
Traduções
Uma
teoria formal de funções tonais generalizadas
Formal
theory of generalized tonal functions
Teoría Formal de Funciones Tonales
Generalizadas
![]() Felipe Defensor Martins 1
felipe.defensor.martins@alumni.usp.br
Felipe Defensor Martins 1
felipe.defensor.martins@alumni.usp.br
Universidade de São Paulo, Brasil
Revista
Orfeu
Universidade do Estado de
Santa Catarina, Brasil
ISSN: 2525-5304
Periodicidade: Contínua
vol. 7, núm. 2, 2022
revistaorfeu@gmail.com
Recepção: 11 Maio
2022
Aprovação: 12 Julho
2022
Autores mantém os
direitos autorais e concedem à revista o direito de primeira publicação.
![]()
Este trabalho está sob uma Licença Internacional Creative Commons Atribuição 4.0.
Resumo: Tradução
do seminal artigo A Formal Theory of
Generalized Tonal Functions
de David Lewin, publicado em 1982, que prefigura algumas ideias mais tarde
desenvolvidas em Generalized Musical Intervals and Transformations
(LEWIN, 1987) e que dariam origem à teoria transformacional e à teoria neorriemaniana. No artigo é construída, por meio de
formalização matemática, uma estrutura denominada Sistema Riemann, que
generaliza certos conceitos pertinentes à teoria da música tonal, como o de
função harmônica e o de função melódica. São também conceituadas transformações
que relacionam Sistemas Riemann entre si, abarcando e estendendo o escopo das
transformações riemanianas tradicionais. Tais
transformações podem ser interpretadas como correspondentes a outras noções
teóricas familiares, como a transposição, a inversão, o “se tomar a relativa”,
o “se tomar a mediante”, entre outras. Algumas pequenas análises de excertos de
Wagner, Brahms, Stravinsky e Beethoven são elaboradas a título de mostrar a
pertinência da teoria desenvolvida para a análise musical.
Palavras-chave: Funções Tonais
Generalizadas, David Lewin, teoria transformacional, Hugo Riemann, análise
musical.
Abstract: Translation of
the seminal article A
Formal Theory of Generalized Tonal Functions by David Lewin, published in
1982, which foreshadows
some ideas later developed
in Generalized Musical Intervals
and Transformations (LEWIN,
1987) and which would give rise
to transformational theory and neo-Riemanian
theory. The author builds, through mathematical formalization, a structure called the Riemann System, which generalizes certain concepts pertinent to the theory
of tonal music, such as harmonic function and melodic
function. Transformations that relate Riemann Systems to each other are also conceptualized, embracing and extending
the scope of traditional Riemannian transformations. Such transformations can be interpreted
as corresponding to other familiar theoretical notions, such as transposition, inversion, “taking the relative”,
the “taking the mediant”, among
others. Some short analyzes
of excerpts from Wagner, Brahms, Stravinsky and
Beethoven are elaborated in order
to show the relevance of the
theory developed for
musical analysis.
Keywords: Generalized Tonal Functions,
David Lewin, transformational theory,
Hugo Riemann, musical analysis.
Introdução
O texto a seguir é uma tradução do artigo A Formal Theory of Generalized
Tonal Functions de David B. Lewin, publicado pela
Duke University Press em 1982 no primeiro número do
26º volume do Journal of
Music Theory. O artigo é conhecido por apresentar o
embrião de ideias que seriam posteriormente desenvolvidas em Generalized Musical Intervals and Transformations, a obra mais
influente do autor, que inaugura a teoria transformacional e prefigura o que se
conhece atualmente como teoria neorriemaniana. Além
de seu caráter precursor, Generalized Tonal Functions traz uma construção teórica com valor autônomo, o
Sistema Riemann, que generaliza diversos aspectos tradicionais da teoria sobre
música tonal.
David B. Lewin (1933–2003) foi um compositor, intérprete e
prolífico teórico americano, já chamado de “o mais original e abrangente
teórico de sua geração” (COHN, 2001).
Graduado em matemática pela Universidade de Yale, estudou composição com Roger Sessions e teoria com Milton Babbit
(COHN, 2001). É o mais relevante pesquisador da segunda geração de teóricos do
que hoje conhecemos como teoria pós-tonal, seus escritos englobam, entre outros
assuntos, o desenvolvimento de formalizações matemáticas voltadas para teoria e
análise musical (e.g. (LEWIN, 2007)),
análise musical propriamente dita (LEWIN,
1993) e metodologia da teoria e análise musical (LEWIN, 1969, 1986).
Um Sistema Riemann, o construto matemático central de A Formal Theory of
Generalized Tonal Functions,
é elaborado pela generalização de um método comum de se obter “um sistema de
funções e relações tonais” a partir de uma tônica, de um intervalo dominante e
de um intervalo mediante. Essa construção permite que sejam generalizados,
entre outros, os tradicionais conceitos de tônica, dominante, subdominante,
mediante e submediante. Lewin também relaciona os
Sistemas Riemann entre si por certas operações. Algumas delas correspondem a
conceitos familiares como “tomar a tonalidade relativa”, “tomar a tonalidade
dominante”, “transpor por N semitons” e “inverter” enquanto outras estabelecem
relações originais. Combinando as transformações de certas maneiras, é possível
obter diversos grupos, no sentido matemático, antecipando o papel que esse
conceito viria a ter em Generalized Musical Intervals and
Transformations (LEWIN, 2007). Relevante também é o fato de
que três dessas operações (TDINV, TMINV e MDINV) se tornariam posteriormente as
operações neorriemanianas básicas P, L e R. O artigo
também conta com breves exemplos de aplicações analíticas dos conceitos
trabalhados, em composições de Wagner, Brahms, Stravinsky e Beethoven.
Uma Teoria Formal de
Funções Tonais Generalizadas
David Lewin
Nosso ponto de partida é um método comum para construir um
sistema de relações e funções tonais, dados uma classe de altura tônica T, um
intervalo dominante[2] d e um intervalo mediante
m. Esse método é retratado na Fig. 1.
Na Figura, vemos um
sistema de Dó maior[3] construído dados a classe
de altura tônica T = C, o intervalo dominante d =
quinta (módulo a oitava) e o intervalo mediante m = terça maior (módulo a
oitava). Da nota tônica., construímos notas distantes por um intervalo de
dominante e um intervalo de mediante, isto é, G = C+d e e = C+m.
Junto com a nota tônica, essas notas, dominante e mediante, constituem a tríade
tônica do sistema. Em seguida construímos uma tríade dominante, que consiste na
nota dominante G junto com as notas D = G+d e b = G+m que distam
os intervalos d e m, respectivamente, de .. De forma
similar, construímos uma tríade subdominante abarcando a nota tônica ., a nota subdominante F da qual C dista o intervalo
., e a nota submediante a, que dista o intervalo m da
nota subdominante .. Como F é construída para satisfazer a relação F+d = C,
podemos escrever simbolicamente F = C-d; dessa
maneira a = F+m = C-d+m.
A união pela teoria dos conjuntos das três tríades geradas até o
momento pode ser denominada “conjunto diatônico” para o sistema, isto é, o
conjunto não-ordenado composto pelas sete classes de altura sob consideração. O
método de geração sugere um ordenamento específico para o conjunto diatônico,
condensando e agrupando a estrutura desenvolvida na parte superior da Fig. 1. Essa ordenação é exibida pela série FaCeG♭.
na parte inferior da Figura. A série será chamada de “lista canônica” para o
conjunto diatônico do sistema que está sendo construído. Letras maiúsculas são
utilizados para denotar classes de altura geradas pela nota tônica e por vários
múltiplos do intervalo dominante: C, F = C-d, G = C+d, D = G+d = C+2d.
Letras minúsculas denotam classes de altura cuja geração envolve o intervalo de
mediante: e = C+m, b = G+m, a = F+m.
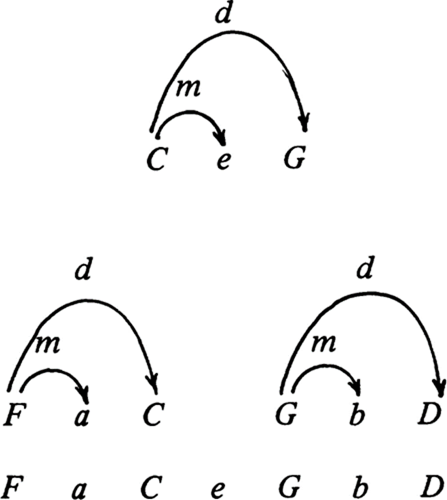
Figura
1
Construção
de um sistema de Dó maior
Certas características do sistema, como será notado, são
condições necessárias do próprio método construtivo, independente dos tamanhos
de d e m. Por exemplo, as tríades dominante e subdominante devem
necessariamente ser formas transpostas da tríade tônica. O intervalo da nota
mediante T+m para a nota tônica T deve ser -m,
e o intervalo da nota mediante T+m para a nota submediante T-d+m deve
ser -d; dessas relações, segue que a “tríade submediante”, isto é, o conjunto que abarca as notas T-d+m, T e
T+mT + m, deve ser uma inversão da tríade
tônica. E assim por diante.
Para além de tais características internas necessárias do
sistema, o método construtivo também induz algumas relações formais necessárias
entre o sistema e certos sistemas construídos de forma similar. Por exemplo, o
sistema da Fig. 1, cuja lista canônica é FaCeGbD, possui certas relações necessárias com
outros sistemas de construção similar, por exemplo, aqueles com as listas
canônicas FA.Ce.Gb.D, Db.Ge.Ca.F, CeGbDf#A,
DfAcEgB, e assim por diante.
Nesse artigo, iremos generalizar os métodos construtivos
adotados para a Fig. 1. Veremos até que ponto características tradicionais da
teoria tonal dependem formalmente apenas desse método, ao invés dos d e m
específicos. Iremos explorar alguns sistemas não-tonais que podem ser
construídos pelo método, sistemas para os quais características pertinentes e
análogas valem. Tais sistemas, ao mesmo tempo que iluminam as características
formais análogas da teoria tonal, também sugerem possibilidades interessantes
de composição e análise por si mesmos.
Há uma longa e rica tradição na história da teoria tonal por
trás da Fig. 1. A abordagem formalista da discussão acima sobre questões como
as interrelações de tríades e sistemas pode ser particularmente associada com o
espírito e trabalho de Hugo Riemann. Por essa razão, chamarei a estrutura
abstrata básica que estudaremos de “Sistema Riemann” (daqui em diante “SR”)[4].
Sistemas Riemann. Todas as notas e
intervalos serão entendidas módulo a oitava, a menos que dito o contrário. Para
adotar uma convenção consistentemente, usaremos notação aditiva para
intervalos, como na discussão da Fig. 1. Portanto se X é uma classe de altura e
i é algum intervalo (cada qual módulo a oitava) então X+i é uma classe de
altura tal que o intervalo entre X+i de X é i, assim como o intervalo entre X-i e .. Como o contexto pode sugerir, i pode ser imaginado como
medido em semitons temperados módulo 12, ou em cents
módulo 1200, ou como o logaritmo de uma razão justa módulo log2, e assim por diante.
DEFINIÇÃO 1. Por um
Sistema Riemann (SR) entenderemos um trio ordenado
(T, d, m), onde T é uma classe de altura e d e m são intervalos, sujeitos às
restrições de que d ≠ 0, m ≠ 0, e m ≠ d.
As restrições são necessárias e suficientes para garantir que as
classes de altura T, T+m e T+d
serão distintas, de maneira que possamos falar de “tríade” sem desconforto[5]. T será chamada de “classe de altura tônica” do
sistema; d e m são seus “intervalos dominante e mediante”.
DEFINIÇÃO 2. A tríade tônica do SR (T, d, m) é o conjunto não-ordenado
(T, T+m, T+d). A tríade dominante do sistema é (T+d,
T+d+m, T+2d). A tríade de
subdominante do sistema é (T-d, T-d+m, T). Essas tríades são as
tríades primárias do sistema.
Pode-se ver que as tríades primárias são formas transpostas,
cada uma de qualquer outra.
DEFINIÇÃO 3. O conjunto diatônico de (T, d, m) é o resultado da união
(pela teoria dos conjuntos) não-ordenada das
tríades primárias, abarcando as várias classes de altura T-d,
T-d+m, T, T+m, T+d, T+d+m, e T+2d.
Dadas as restrições da Definição 1, pode haver de três a sete (classes de altura) distintas no conjunto
diatônico. Por exemplo, se d é exatamente um terço da oitava, então T-d e T+2d
serão a mesma nota, aqui representando duas funções distintas:
subdominante e dominante da dominante.
DEFINIÇÃO 4. A
lista canônica para (o conjunto diatônico) do SR (T, d, m) é a série ordenada (T-d, T-d+m, T, T+m, T+d, T+d+m,
T+2d).
Essa série ordenada sempre terá exatamente sete entradas, mesmo
que a mesma nota seja inserida mais de uma vez. Por exemplo, se d é exatamente
a metade de uma oitava e m é exatamente um quarto de uma oitava, então a lista
canônica para (C, d, m) pode ser escrita como F#aCe♭.♭.♭♭.♭♭,
com a convenção de que F# e .♭
são a mesma classe de altura, e assim por diante. Essa série tem sete entradas,
representando as sete funções do sistema, mas o conjunto diatônico não-ordenado
tem apenas quatro notas distintas.
O método construtivo discutido até aqui está visualmente
representado na Fig. 2, que generaliza a Fig.
1.

Figura
2
Construção generalizada de um Sistema Riemann
As tríades primárias estão retratadas na lista canônica no fim
da Fig. 2, como as entradas 1 a 3, 3 a 5 e 5 a 7 naquela lista. Os conjuntos de
três notas compreendendo as entradas 2 a 4 e as entradas 4 a 6 também
desempenham papéis formais na generalização da situação tonal. A Definição 5
fornece as formalidades.
DEFINIÇÃO 5. A tríade mediante do SR (T, d, m) é um conjunto
não-ordenado (T+m, T+d, T+d+m). A tríade submediante é o
conjunto não-ordenado (T-d+m, T, T+m).
Essas são as tríades secundárias do sistema.
Como já notamos, as tríades secundárias são necessariamente
formas invertidas das tríades primárias.
O conjunto não-ordenado que compreende as entradas 7, 1 e 2 na
listagem canônica, isto é T+2d, T-d
e T-d+m, não tem, necessariamente, a forma de
uma tríade secundária. De fato, ele nem precisa ser composto de três classes de
alturas distintas. Por exemplo, se m = 3d (módulo a
oitava), então -d+m+2d e T-d+m =
T+2d. Para que T+2d, T-d
e T-d+m formem um conjunto de tipo tríade
secundária, é necessário e suficiente que T-d+m esteja a um intervalo dominante de T+2d, isto é, que T-d+m seja igual a (T+2d)+d,
ou seja, que T-d+m seja
igual a T+3d. Um pouco de aritmética mostra que
este será o caso se e somente se m for igual a 4d.
A condição é satisfeita pela tonalidade maior temperada, usando qualquer
temperamento em que a “terça maior” seja equivalente a quatro “quintas”, módulo
a oitava. A condição, no entanto, não é característica de Sistemas Riemann em
geral[6].
Sistemas redundantes e irredundantes
DEFINIÇÃO 6. Um
Sistema Riemann será chamado redundante se o seu
conjunto diatônico tem menos de sete membros e irredundante se o seu
conjunto diatônico tem exatamente sete membros.
A Tab. 1 lista alguns Sistemas Riemann
redundantes, usando temperamento igual de doze alturas e medindo intervalos em
semitons iguais. As listas canônicas da Tabela usam nomes de letras para
classes de altura, com as convenções usuais sobre grafia enarmônica. Os
conjuntos diatônicos na tabela são escritos usando a notação inteira para
classes de altura (0 para ., 1 para C#, ... , 11 para .).
A Tab. 1 mostra que o conjunto diatônico de
um Sistema Riemann redundante tem 3, 4, 5 ou 6 membros. A Tabela também mostra
como alguns conjuntos de classes de alturas interessantes dessas cardinalidades
podem ser gerados como conjuntos diatônicos para vários Sistemas Riemann. Isto
pode se mostrar interessante na análise ou composição de música que envolva
esses conjuntos. Um conjunto de classes de altura particular pode ser o
conjunto diatônico para mais de um tipo de Sistema Riemann: por exemplo, a
escala de tons inteiros é gerada por dois sistemas essencialmente diferentes na
Tabela.

Tabela
1
Alguns Sistemas Riemann redundantes
Uma questão teórica natural surge: quais são as condições
necessárias e suficientes sobre d e m para que o Sistema Riemann (T, d, m) seja irredundante? O
Teorema 1 responde a essa pergunta.
TEOREMA 1. Para o
SR (T, d, m) ser irredundante é necessário e
suficiente que as condições (1) e (2) que seguem sejam satisfeitas.
(1) Para N = 1, 2
ou 3, Nd não é zero. (Isto é, um, dois ou três
intervalos dominante não somam um número exato de oitavas. Isso é, d não é 0,
6, 4, ou 8 semitons temperados por igual.)
(2) Para N = 0, ±1,
±2 ou ±3, m não é igual a Nd. (Esta condição não
exclui a possibilidade que m possa ser igual a -3d.)
O teorema pode ser verificado por uma inspeção sistemática das
várias relações intervalares entre as várias notas T-d, T-d+m,
T, T+m, T+d, T+d+m, e T+2d. Por exemplo, T-d e T+d+m,
são a mesma nota se e somente se -d = d+m
o que é o caso se e somente se m = -2d. A Tab. 2 abaixo lista essencialmente todos os Sistema Riemann irredundantes no temperamento igual de doze alturas. O
significado preciso de “essencialmente” aqui ficará claro durante a discussão
subsequente.
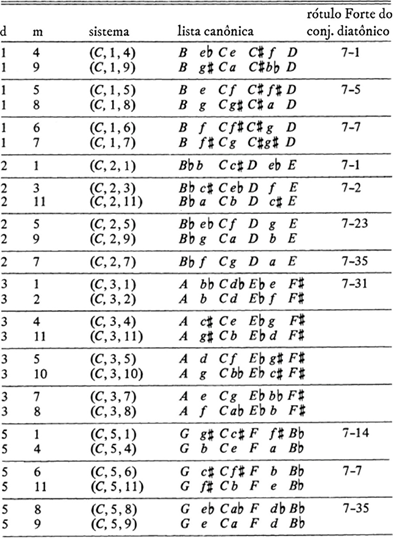
Tabela
2
Todos os Sistemas Riemann (essencialmente)
As duas primeiras colunas da Tab. 2 contêm todas as combinações
de valores para d e m que atendem às condições do Teorema 1, de d = 0 até d = 5. Por exemplo,
d = 1 é permitido pela condição (1) do Teorema;
para d = 1, a condição (2) não permite m = 1, m = -1 (= 11), m = 2, m = -2 (= 10) e m = 3. Os
demais valores possíveis para ., ou seja, m = 4, 9, 5, 8, 6 e 7, estão listados na segunda coluna
da tabela, ao lado de d = 1 na primeira coluna. A ordem em que esses valores
para m estão listados será discutida mais adiante. Veremos que é suficiente
listar apenas na tabela os valores de d a d = 0 até
d = 5: sistemas irredundantes
com d = 7, 9, 10 ou 11 podem
ser derivados de sistemas com d = 5, 3, 2 ou ., respectivamente. A terceira coluna da Tab. 2 contém os
nomes dos sistemas Riemann com nota[7] tônica C e
intervalos dominante e mediante correspondentes às entradas na
primeira e segunda colunas da tabela. A quarta coluna contém as
listagens canônicas geradas pelos Sistemas Riemann inseridos na coluna três. As
convenções usuais de grafia de equivalência enarmônica são adotadas. A última
coluna contém os rótulos Forte[8] para os tipos
de acordes dos conjuntos diatônicos em questão[9].
Quando nenhum rótulo aparece na coluna cinco da Tabela, entende-se que o último
rótulo escrito acima se aplica. Por exemplo, o tipo do conjunto diatônico para
(., 1, 8) é 7–5; o tipo do conjunto diatônico de (., 3, 10) é 7–31.
Com duas exceções, cada sistema na Tab. 2 é pareado com outro
sistema, que iremos chamar de seu “sistema conjugado.” As exceções são (., 2,
1) e (C, 2, 7): cada um desses sistemas é o seu próprio conjugado. Para ver o
aspecto matemático saliente da relação de conjugação, observe que (., 1, 4) e
(., 1, 9) estão pareados, e que 4+9 = 1. (., 1, 5) é pareado com (., 1, 8), e
5+8 = 1. (., 2, 3) é pareado com (., 2, 11), e 3+11 = 2. (., 3, 7) é pareado
com (., 3, 8), e 7+8 = 3. (., 2, 1) é auto-conjugado,
e 1+1 = 2. Em geral, (T, d, m) e (T, d, m’) são
sistemas conjugados se m+m’ = d. Algumas definições formais são necessárias.
DEFINIÇÃO 7. O sistema conjugado do SR (T, d, m) é o Sistema (T, d, d-m). A operação que transforma um dado SR em seu conjugado
será chamada “CONJ”. Escreveremos, simbolicamente, CONJ(T,
d, m) = (T, d, d-m).
A operação de conjugação pode ser aplicada a qualquer Sistema
Riemann, irredundante ou redundante. Formalmente, é
necessário verificar que (T, d, d-m)
é, de fato, sempre um “Sistema Riemann” sempre que (T,
d, m) o é. Isto é, deve-se verificar se d ≠ m, d-m ≠ 0, e d ≠ d-m,
supondo que d ≠ 0, m ≠ 0 e d ≠ m.
Isso é feito facilmente. Ao discutirmos transformações
subsequentes de Sistemas Riemann, devemos sempre considerar que tais pormenores
metodológicos foram levados a cabo.
Dado um Sistema Riemann (T, d, m),
vamos definir m’ = d-m. O
sistema conjugado articula o intervalo dominante d, dentro de cada tríade
primária, como d = m’+m, em vez de como d = m+m’. Veja a
Fig. 3.

Figura
3
Articulação do intervalo d nos sistemas original e conjugado
A relação entre as subdivisões original e conjugada do intervalo
., assim, generaliza noções tradicionais tais como a divisão
aritmética-versus-harmônica de ., e relações tradicionais tais como a de CeG para
Ce.G[10].
Estendendo o formato da Fig. 3 para abarcar
as listas canônicas comple-tas dos sistemas em
análise, obtêm-se a relação retratada visualmente pelos dois terços superiores
da Fig. 4.
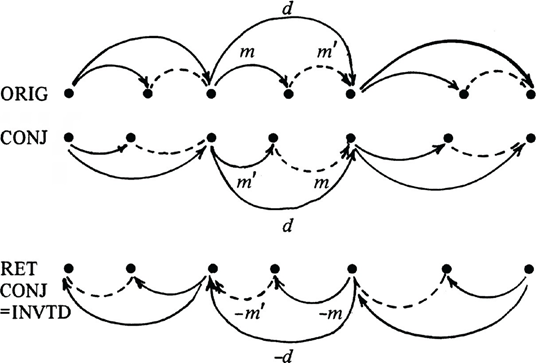
Figura
4
Articulação
dos intervalos m e m’ nos sistema original conjugado e retrógrado do conjugado
Leiamos agora a lista conjugada de trás para frente. Isso produz
uma lista para um sistema “conjugado retrógrado”. Como a parte inferior da Fig.
4 indica, este sistema tem o intervalo dominante -d e
intervalo mediante -m. Neste sentido, é uma
inversão de um determinado sistema. Na verdade, a lista canônica para o sistema
RETCONJ é uma inversão serial da lista canônica
para o sistema original. A Fig. 4 esclarece esta relação: as sete notas
sucessivas da lista original abrangem os seis sucessivos intervalos m, m ‘, m, m ‘, m, m ‘, enquanto as sete notas sucessivas
da lista do conjugado-retrógrado (lendo da direita para a esquerda, na parte
inferior da Fig. 4) abrangem os seis intervalos sucessivos -m, -m’, -m, -m’, -m, -m’. Como a Fig. 4 indica, a nota
tônica do sistema conjugado-retrógrado é a nota dominante do sistema original;
da mesma forma a nota dominante do sistema conjugado-retrógrado é a nota tônica
do sistema original. Já que a relação conjugado-retrógrado troca as notas
tônica e dominante dos sistemas envolvidos, enquanto inverte serialmente as
listas canônicas envolvidas, nós iremos chamar a transformação “Inversão-TD”.
DEFINIÇÃO 8. A inversão-TD do SR (T, d, m) é o Sistema Riemann (T+d, -d, -m). A transformação que leva qualquer SR à sua
inversão-TD será chamada “INVTD”. Escreveremos, simbolicamente, INVTD(T, d, m) = (T+d, -d, -m).
Vamos agora voltar à Tab. 2. Ao lermos as várias listas
canônicas na quarta coluna da tabela de trás para frente, estaremos lendo, en masse, as listas canônicas para as inversões-TD dos
diversos Sistemas que aparecem na coluna 3 da Tabela. Por exemplo, o Sistema
Riemann de Fá maior (., 7, 4) tem a nota dominante .;
portanto, ele é a inversão-TD do Sistema (C, -7, -4) = (C, 5, 8). Como o
inversão-TD de (., 5, 8), (., 7, 4) também é o retrógrado-conjugado de (., 5,
8). Portanto, a lista para (., 7, 4) pode ser lida, na Tab. 2, como o
retrógrado da lista para o sistema conjugado de (., 5, 8), que é como o
retrógrado da lista para (., 5, 9).
Generalizando esse exemplo, podemos ver agora em que sentido a
Tab. 2 lista “essencialmente” todos os tipos de Sistemas Riemann irredundantes no temperamento igual de doze alturas. Se d =
1, 2, 3 ou 5 e o par (d, m) satisfaz as condições
do Teorema 1, então o Sistema (C, d, m) aparece
diretamente na Tab. 2. Se d = 7, 9, 10 ou 11 e o par (d,
m) satisfaz as condições do Teorema 1, então o par (-d,
-m) também irá satisfazer as condições do Teorema, de forma que o
Sistema (C, -d, -m) aparecerá na Tabela. Pode-se em
seguida ler a lista canônica para um Sistema com intervalo dominante d e
intervalo mediante ao se ler de trás para frente a lista canônica para o
sistema conjugado de (C, -d, -m) da Tabela.
Já que o retrógrado da lista conjugada é uma inversão serial de
uma determinada lista, segue que a lista conjugada em si é uma inversão
retrógrada dessa mesma lista. Esta propriedade é facilmente vista e ouvida como
manifestada entre as listas da Tab. 2; ela explica por que
as listas pareadas na Tabela soam tão intimamente relacionadas.
Dado um Sistema Riemann e o seu conjugado, uma vez que as listas
canônicas de seus conjuntos diatônicos são inversões-retrógradas uma da outra
segue que os próprios conjuntos diatônicos não-ordenados têm de ser inversões
de classe de altura um do outro. Portanto, se os Sistemas são irredundantes, eles terão o mesmo número Forte inserido na
coluna 5 da Tab. 2.
Também se pode ver por que a cada Sistema Riemann irredundante que aparece na Tabela com intervalo dominante
d = 3 deve ter 7-31 como o número Forte de seu conjunto diatônico. Em tal
Sistema, as notas T-d, T, T+d
e T+2d serão T-3, T, T+3 e T+6; estas quatro notas constituirão uma “acorde de
sétima diminuta.” E as três notas de T-d+m, T+m e T+d+m vão constituir uma
“tríade diminuta”, que será disjunta do acorde de sétima diminuta (já que o
Sistema é irredundante.) Portanto, as sete notas do
conjunto diatônico formarão uma escala octatônica com
uma nota a menos, e qualquer coleção desse tipo deve ter a forma Forte 7–31.
Ignorando relações de conjugação, o número Forte 7–7 aparece, essencialmente,
duas vezes na quinta coluna da Tab. 2. Isto está evidentemente relacionado com
a presença de trítonos nas listas canônicas
envolvidas. Os Sistemas Riemann cujos conjuntos diatônicos têm esse tipo Forte
são precisamente aqueles Sistemas irredundantes (!)
(T, d, m) tais que m = 6 ou m’ = d-m = 6.
É interessante que o número Forte 7-35 apareça essencialmente
duas vezes na Tabela, uma vez para o “círculo de quintas” (Sistema de ., 2, 7) e uma para os Sistemas “tonais” (invertidos) (.,
5, 8) e (., 5, 9). Vê-se a importância do temperamento como um meio de
conciliar as afinações Pitagórica e justa que as listas canônicas respectivas
mais “naturalmente” sugerem. Os sistemas que compartilham o número Forte 7–1 na
coluna 5 são as transformações pelo círculo das quintas[11]
daqueles que partilham o número Forte 7-35.
Os sistemas irredundantes da Tab. 2, assim como os sistemas redundantes da Tab.
1, podem mostrar-se úteis para a análise de música apropriada; eles também
sugerem interessantes possibilidades de composição.
O grupo serial. Quando dizemos que a
inversão-TD de um Sistema Riemann é o “conjugado-retrógrado”
do sistema, estamos, implicitamente, invocando a noção de transformação de um
Sistema, e não apenas de uma lista, por uma operação chamada de “retrogradação.” Devemos agora ser mais formais em relação a
esta noção. Por “sistema retrógrado” de um determinado SR (T,
d, m) nós claramente nos referimos ao SR cuja lista canônica é o
retrógrado da lista canônica para (T, d, m). A Fig.
5 apresenta algumas características salientes da estrutura envolvida.
Inspecionando a Fig. 5, vemos que a nota
tônica do sistema retrógrado será a nota dominante T+d do sistema
original. O intervalo dominante do sistema retrógrado será -d, e o seu intervalo mediante -m’,
onde m’ = d-m. Podemos
colocar tudo isso em uma definição formal.
DEFINIÇÃO 9. O retrógrado do SR (T, d, m) é o Sistema Riemann (T+d, -d, m-d). As transformações que levam qualquer SR ao
seu retrógrado serão chamadas “RET”. Escreveremos, simbolicamente, RET(T, d, m) = (T+d, -d, -m).
Será útil agrupar vários aspectos das Figs.
3, 4 e 5 na Fig. 6, que apresenta algumas interrelações entre as estruturas das
tríades primárias de um Sistema Riemann original, seu retrógrado, seu conjugado
e a sua inversão-TD.
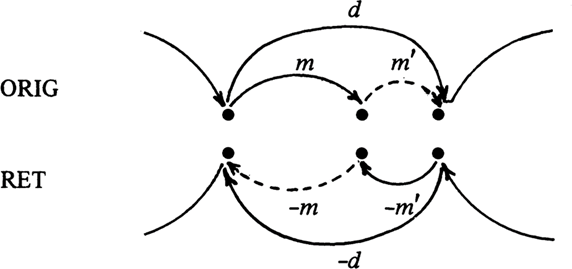
Figura 5
Articulação dos intervalos m e m’ nos sistemas original e retrógrado
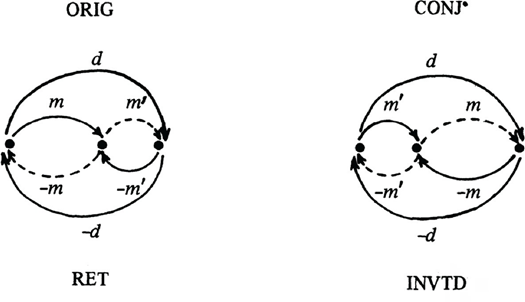
Figura
6
Articulações dos intervalos m e -m nos sistemas original, conjugado,
TD-invertido e retrógrado, formando uma coleção simétrica
Como a Fig. 6 sugere, visualmente, a
conjunção de um Sistema Riemann com seu sistema conjugado, TD-invertido e
retrógrado dá origem a uma coleção simétrica e fechada de Sistemas Riemann
mutuamente interdependentes. Podese ouvir isto nas
características que agrupam auditivamente qualquer par de listas conjugadas e
seus retrógrados, na Tab. 2, como distintas de todas as outras listas naquela
tabela. A concisão e a simetria sugeridas pela Fig. 6 refletem o fato de que as
operações CONJ, INVTD e RET, juntamente com a
operação de “deixar estar” um sistema, formam o que os matemáticos chamam de um
“grupo de operações” na família de todos os Sistemas Riemann. Vamos examinar
mais a fundo as implicações deste fato. Primeiro, precisamos de um rótulo
formal para a operação de “deixar estar” qualquer Sistema Riemann, produzindo o
determinado Sistema, idêntico, como resultado da operação.
DEFINIÇÃO 10. Pela operação identidade na família de Sistemas Riemann, nos
referimos a operação IDENT que, quando aplicada ao espécime SR(T,
d, m), produz como resultado (T, d, m) ele mesmo. Escreveremos, simbolicamente,
IDENT(T, d, m) = (T, d, m).
Exploraremos agora várias relações que são verdadeiras entre
combinações de operações de IDENT, INVTD, RET e CONJ.
Os tipos de relações que nos dizem respeito, aqui, são aquelas que podem ser
expressas por o que chamaremos de equações
operacionais. Um exemplo de uma dessas equação é a afirmação simbólica RET CONJ = INVTD. Esta equação coloca que o retrógrado do
conjugado, de qualquer SR dado, é o mesmo Sistema que sua inversão-TD. A
declaração é verdadeira, como recordamos da discussão pertinente anterior (ver
discussão que acompanha as Definições 7 e 8). Podemos também demonstrar a
veracidade da afirmação aplicando algumas substituições e manipulações
algébricas às definições das operações envolvidas. Realizarei esta demonstração
no parágrafo seguinte, para aqueles leitores que estão interessados; aqueles
que não estiverem podem omitir ou postergar o estudo deste exercício, que é
paradigmático para a demonstração rigorosa da verdade de tais equações.
Devemos mostrar que, dado qualquer Sistema Riemann (T, d, m), o Sistema RET(CONJ(T, d, m)) é o
mesmo que o Sistema INVTD(T, d, m). Vamos denotar
por (T#, d#, m#)), o Sistema CONJ(T,
d, m); em seguida, devemos mostrar que RET(T#, d#,
m#)) é o mesmo sistema que INVTD(T, d, m).
Invocando a Definição 9, inferimos que devemos mostrar a relação (T#+d#, -d#, m#-d#) = INVTD(T, d, m). Agora
(T#, d#, m#) é o conjugado de (T,
d, m); pela Definição 7 sabemos que esse último Sistema é (T, d , d-m); portanto T# = T, d# = d e m# = d-m.
Fazendo essas substituições, conforme apropriado, vemos que o Sistema (T#+d#, -d#, m#-d#) é o Sistema (T+d, -d, (d-m)-d) ou (T+d, -d, -m). Então, o que
devemos mostrar é que (T+d, -d,
-m) = INVTD(T, d, m). E esse é de fato o caso,
conforme indicado pela Definição 8.
Outro exemplo de uma equação operacional é RET
RET = IDENT. Esta equação afirma que o sistema
retrógrado do sistema retrógrado de um dada RS, é idêntico ao dado SR em si. A
veracidade da equação é facilmente intuída considerando as listas canônicas
envolvidas. Pode-se também provar a equação pelas técnicas de substituição e
álgebra utilizadas para a prova do exemplo anterior. Vê-se no formato da
presente equação a utilidade de ter uma operação formal chamada IDENT para
participar de tais relações.
As equações básicas que se dão entre os membros de nossa família
de quatro operações podem ser apresentadas sinopticamente pela Tab.
3, a qual matemáticos poderiam chamar de uma “tabela de combinação” para a
família. O formato da Tab. 3 é similar ao de uma tabela de multiplicação
corriqueira: se a operação Z é inserida na tabela, na fileira com X na extrema
esquerda e na coluna com Y como cabeçalho, então a equação operacional X Y = Z
é verdadeira. Por exemplo, na fileira da Tab. 3 com INVTD na esquerda, e na
coluna RET encabeçada por RET, encontramos a entrada CONJ. Isto significa que a
equação INVTD RET = CONJ é verdadeira. I.e.: a inversão-TD do sistema
retrógrado, de qualquer SR dado, é o sistema conjugado desse dado SR.
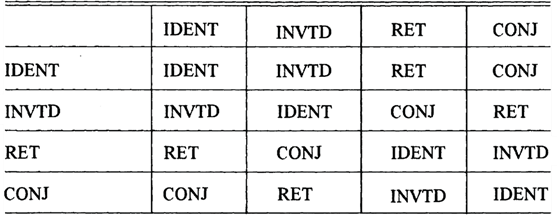
Tabela 3
Tabela
de combinação para as operações IDENT, INVTD, RET e CONJ
Analisando a Tab. 3, é fácil verificar que a família composta
IDENT, INVTD, RET e CONJ forma um grupo de operações, no sentido matemático.
Ela satisfaz os dois requisitos que uma família (não vazia) de operações deve
satisfazer para formar um grupo. Primeiro, os membros da família, combinados
entre si, sempre irão produzir um resultado que é operacionalmente igual a
algum membro da família: eles não irão gerar quaisquer operações novas quando
aplicados um após o outro. Formalmente, se X e Y são membros da família
(possivelmente o mesmo membro), então existe um Z na família (possivelmente o
próprio X ou Y) que satisfaz a equação operacional X Y = Z.
Segundo, para cada membro X da família, há algum membro Y da
família (possivelmente X) que satisfaz as equações X Y = Y X = IDENT. Nesta
situação, Y é exclusivamente determinado por X; é chamado de “(operação)
inversa” de X. Dado X e seu inverso Y, se X transforma o operando 1 no operando
2, então Y transforma o operando 2 no operando 1. Já que (operando 2) = Y(X(operando 1)) = IDENT(operando 1) = operando 1. Assim,
dado um par de operações inversas, cada uma “desfaz” o efeito da outra. No caso
da família envolvida na Tab. 3, cada membro-operação se combina com si mesmo
para formar a operação identidade e, portanto, é seu próprio inverso, se
“desfazendo” quando aplicado uma segunda vez após a sua primeira aplicação.
DEFINIÇÃO 11. A
família que compreende as quatro operações IDENT, INVTD, RET e CONJ será
chamada de grupo serial de operações sobre (o
conjunto de todos os) Sistemas Riemann. O grupo será denotado por GSER.
O nome que eu dei a este grupo surge dos efeitos que suas
operações induzem em uma lista canônica de um determinado Sistema. Como já
observamos, as operações citadas na Definição 11 preservam, invertem,
retrogradam e retrogradam-invertem, respectivamente, a lista canônica de um
determinado SR em listas canônicas dos Sistemas respectivamente transformados.
Este aspecto do grupo serial relaciona certas transformações tonais tradicionais,
quando generalizado, a outras conhecidas estruturas transformacionais
normalmente consideradas apenas no contexto de músicas ocidentais mais
recentes. Essa relação, em seus aspectos tanto formais quanto
histórico-culturais, é certamente mais do que fortuita. Ela justifica, penso
eu, uma reflexão mais profunda. Por agora, vamos apenas observar que o aspecto
“serial” de GSER é crucialmente dependente da ordenação para conjuntos
diatônicos dada pelo conceito de lista canônica; uma organização escalar dos
conjuntos diatônicos envolvidos obscureceria, em vez de revelar, a função
estrutural das transformações seriais.
Dados Sistemas Riemann SR1 e SR2, iremos definir que “SR2 é uma
forma de SR1 (mod GSER)” quando algum membro de GSER
transforma SR1 em SR2, isto é, quando algum membro X de GSER satisfaz X(SR1) =
SR2. Devido à homogeneidade induzida pela estrutura do grupo, essa relação
entre os Sistemas Riemann é tanto simétrica quanto transitiva. Isto é, se
X(SR1) = SR2, então Y(SR2) = SR1, onde Y é o inverso de X; então, se SR2 é uma
forma de SR1, SR1 é uma forma de SR2 (mod GSER). E
supondo que X(SR1) = SR2 e Y(SR2) = SR3, X e Y sendo membros de GSER, segue-se
que Z = YX é um membro de GSER, tal que Z(SR1) = SR3; assim se SR2 é uma forma
de SR1 e SR3 é uma forma de SR2, então SR3 é uma forma de SR1 (mod GSER).
Dessas propriedades, um fato importante resulta. Dados quatro
(ou dois) Sistemas Riemann inter-relacionados pelas quatro operações de GSER,
nós não podemos atribuir prioridade estrutural ou formal para qualquer um
desses Sistemas tendo como base exclusivamente a rede de relações-GSER entre
eles; todos podem ser igualmente considerados formas de qualquer um dos outros.
Por exemplo, dados os sistemas (F, 2, 3), (F, 2, 11), (G, 10, 1) e (G, 10, 9),
podemos de fato dizer que o segundo, terceiro e quarto Sistemas são,
respectivamente, o conjugado, retrógrado e inversão-TD do primeiro; mas podemos
também dizer que o primeiro, o segundo e o quarto são, respectivamente, o
retrógrado, a inversão-TD e o conjugado do terceiro, e assim por diante. A
menos que queiramos atribuir prioridade especial por algum outro fundamento
para uma das classes de altura F ou G, ou para algum dos intervalos de 2, 10,
3, 11, 1 e 9, em detrimento de outros, não temos nenhuma maneira de afirmar que
qualquer um dos quatro Sistemas deve ser considerado “primário”, “primo” ou
“básico” e os outros três “derivados” em algum sentido subordinante; no que
concerne relações entre os grupos, qualquer um dos quatro Sistemas pode ser
derivado a partir de outro qualquer de modo absolutamente igualitário.
É útil ter feito esta observação antes de passar a investigar
especificamente os quatro Sistemas Riemann no temperamento igual de doze
alturas que podem ser derivados do Sistema de “Dó maior” (., 7, 4) pelas
operações de GSER: Dó maior é igualmente uma forma derivada de qualquer um dos
outros três Sistemas, que são igualmente formas derivadas de si próprios. A
discussão anterior deixa claro que, se pretendemos atribuir prioridade a Dó
maior em preferência aos outros três Sistemas, é apenas porque desejamos
atribuir prioridade para a “quinta” e a “terça maior” como intervalos
estruturais nesta conexão[12].
O Sistema (., 7, 3) é o conjugado de Dó maior. Vamos chamá-lo de
“Dó menor.” Como já mencionado, a relação de conjugação coloca na terminologia
do presente artigo noções tais como a divisão harmônica e aritmética da quinta,
ou a inversão (renversement)
das tríades maior e menor dentro da quinta.
O Sistema de (., 5, 8) é a inversão-TD de Dó maior. Vamos
chamá-lo de “Sol menor dual.” Sua tríade tônica projeta, desde a nota tônica G,
as notas dominante e mediante C = G+5 e .♭ =
G+8, isto é, as notas, respectivamente, uma quinta e uma terça maior
“abaixo” da tônica. A estrutura será familiar para estudantes das teorias de
Riemann; Riemann recomendou esta tríade como a forma “natural” das tonalidades
menores, apesar de ter recuado de forma um tanto ilógica de chamar Ca♭. de “tríade dominante” de
Ge♭. neste contexto[13].
O Sistema de (G, 5, 9) é o retrógrado de Dó maior. Vamos
chamá-lo de “Sol maior dual.” Sua tríade tônica
projeta, a partir da nota tônica G, as notas dominante e mediante C = G+5, e =
G+9, isto é, as notas, respectivamente, uma quinta e uma terça menor “abaixo”
da tônica. Até onde sei, nenhum aspecto desse sistema foi até agora
investigado, muito menos recomendado, por qualquer teórico da tonalidade. As
formalidades do presente contexto fazem com que essa observação seja um tanto
impressionante. Se admitirmos a cogência musical da
relação “Dó menor = CONJ(Dó maior)” e da relação “Sol menor dual = INVTD(Cmaj),” e se adicionalmente considera-se a tonalidade menor
como sendo tão básica quanto a maior, em vez de estritamente subordinada à
maior, então deve-se admitir como igualmente convincentes relações como “Sol
maior dual = CONJ(Sol menor dual)” ou “Sol maior dual = INVTD(Dó menor)”. Sol
maior dual viria, assim, naturalmente à consideração e, tendo-se admitido duas
espécies de menor que são uma retrógrada da outra, seria nada mais do que
lógico admitir duas espécies de maior que são uma retrógrada da outra, sempre
supondo que se coloque o menor em paridade estrutural com o maior.
Assim, pode-se analisar a ausência de Sol maior
dual na literatura da teoria tonal da seguinte forma. Primeiro, alguns teóricos
consideram a tonalidade maior corriqueira, com d = 7 e m = 4, como tendo uma
forte prioridade, devido a certos aspectos dos intervalos de 7 e 4, ou dos
intervalos justos que eles aproximam. Para esses teóricos, qualquer espécie de
tonalidade menor deve ser considerada como derivada da maior em uma relação
assimétrica de estrita subordinação. Portanto, não se pode fazer
necessariamente as mesmas coisas que fazemos em Dó maior em Dó menor, ou em Sol
dual menor; nem se pode necessariamente fazer a um dos sistemas menores as
coisas que podem ser feitas em Dó maior. Segundo, dentre os teóricos que
consideram ou Dó menor ou Sol menor dual como tendo a mesma prioridade
estrutural de Dó maior, ninguém considera que ambos os sistemas maior e menor
dual tenham essa prioridade simultaneamente. Então, um teórico que dá a Dó
menor um status igual ao de Dó maior, em uma relação simétrica, pode enfatizar
a transformação conjugada como cheia de importância enquanto nega
implicitamente a significância musical da inversão-TD e da retrogradação.
Dó maior e Dó menor são, então, simetricamente relacionados, cada um como o
conjugado do outro. Sol menor dual e Sol maior dual também estão nessa relação,
mas o fato não tem mais significância musical, para tal teórico tonal, do que o
fato de que (., 2, 11) e (., 2, 9), são conjugados: nenhum desses sistemas tem
nada a ver com a “tonalidade” como concebida por tal teórico. Matematicamente,
o grupo tido como significante para a teoria tonal compreenderia apenas os dois
membros IDENT e CONJ. Em um espírito semelhante, um
teórico diferente (tal como Riemann) pode aceitar Dó maior e Sol dual menor
como tendo a mesma prioridade, mas descartar Dó menor e Sol dual maior como
estruturas “tonais”. Nesse caso, Dó maior e Sol menor dual são simetricamente
relacionados pela transformação INVTD. Dó menor e
Sol maior dual também são relacionados por essa
transformação, mas esse fato não tem mais relevância, para tal teoria, do que a
relação INVTD entre os sistemas igualmente
“atonais” (., 1, 9) e (., 11, 3). O grupo que essa teoria tem como relevante
compreende apenas os dois membros IDENT e INVTD.
Vale a pena explorar em que medida o conceito de “dual maior”
faz sentido para a análise de várias passagens tonais. Pessoalmente, eu acho
que faz tanto sentido quanto o de dual menor. Por essa razão, e também porque a
maioria dos leitores americanos contemporâneos irão sem dúvida compartilhar a
minha própria inclinação a não “acreditar em” menor dual, muito menos em “maior
dual”, discutirei uma série de exemplos musicais nos quais eu, pessoalmente,
sinto que faz sentido afirmar o funcionamento dos conceitos de “dual menor” e
“dual maior” ou ambos, pelo menos no que diz respeito à estrutura triádica e, em certa medida, além disso.
O Ex. 1 é retirado da abertura de Sacre du Printemps de
Stravinsky. Dentro da sonoridade agrupada pelas semicolcheias, a altura de
referência é claramente B4[14],
e não E4. B4 participa do gesto geral linear
básico, de C5 passando por B4 e
indo até A4. E4 fica abaixo de B4, assim como G4, ambos em
relação consonante à altura referencial B4. Da
mesma forma, se analisaria a sonoridade de semicolcheias como uma tríade de Si
menor dual: E e G aparecem como uma quinta e uma
terça maior abaixo de .. Certamente se faz violência
ao sentido da passagem se tentamos ouvir E como fundamental para a tríade.

Exemplo
1
Trecho
da abertura de Sacre du Printemps, de Stravinsky.
O Ex. 2, tirado da abertura de Parsifal, de Wagner, mostra uma
situação semelhante no que tange a estrutura descrita pela sucessão G4-C4-(D4)-E♭..
Nossa atenção aqui está em G4, não no C4. G4 foi apenas ouvido como sensível de
.♭.; agora .♭.
torna-se um vizinho superior a G4 e resolve de fato
em G4, revertendo a relação de tendência anterior. C4, e .♭.,
ouvidos recentemente como 3ª e 5ª de uma tríade de .♭,
agora são ouvidas como 5ª e 3ª abaixo do G4, em uma
tríade de Sol menor dual. Tudo isso é um exemplo clássico do que Riemann chamou
de Leittonwechsel.

Exemplo 2
Trecho da abertura de Parsifal, de Wagner.
O Ex. 3 é da abertura do Intermezzo Op. 119, no. 1, de Brahms. Quase parece que o
compositor construiu um exercício acadêmico na projeção composicional não
apenas de tríades duais menores mas, para além disso,
de grandes segmentos seriais da lista canônica inteira do Sistema Riemann de Fá# maior. Pode-se ler estes

Exemplo 3
Trecho
da abertura do Intermezzo Op. 119, no. 1, de Brahms.
A análise faz sentido porque o ouvinte se orienta
harmonicamente, neste contexto, pelos topos e inícios das cadeias de 3ªs, mais
do que por seus pontos baixos e terminações (antecipadas). A passagem sugere
uma modulação a um Sistema maior relacionado, e a peça como um todo explora
tais modulações. Dada a análise da Fig. 7, o Sistema
relacionado certamente não é Ré maior; em vez disso é Lá maior dual: as tríades
maiores em questão são apresentadas e desenvolvidas exatamente da mesma forma
como são as tríades menores. A Fig. 8 tenta analisar a
passagem toda como uma projeção de segmentos da lista canônica de Lá maior
dual. É esta estrutura, e não um Ré maior usual, que está em contenda com a
estrutura da Fig. 7.
A estrutura de Lá maior dual não é
muito poderosa nas quatro primeiras linhas da Fig. 8; torna-se forte, porém na
quinta linha da Fig. 8, mais forte do que o Fá# menor
dual colocado pela quarta linha da Fig. 7 para a mesma música. A sexta linha da
Fig. 8 e a quinta linha da Fig. 7 são de igual poder na disputa para afirmar
suas respectivas estruturas. A contenda aqui não é apenas entre notas tônicas,
mas também, e talvez mais, entre letras maiúsculas e minúsculas para os nomes
das notas em questão: C# ou c#?
a ou .?, e assim por diante. Isto é, uma dada nota é
aqui uma fundamental-ou-quinta de algo (maiúscula) ou é uma terça de algo
(minúscula)? Esta questão, que teria encantado Hauptmann,
destaca o estado único da nota .: ela é maiúscula em
ambas as figuras.
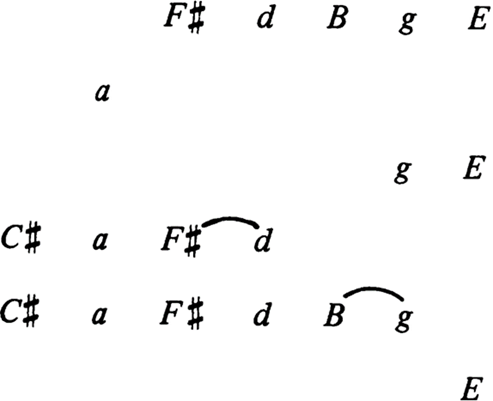
Figura 7
Análise do trecho do Intermezzo Op 119 no 1
de Brahms em relação ao SR de Fá# maior
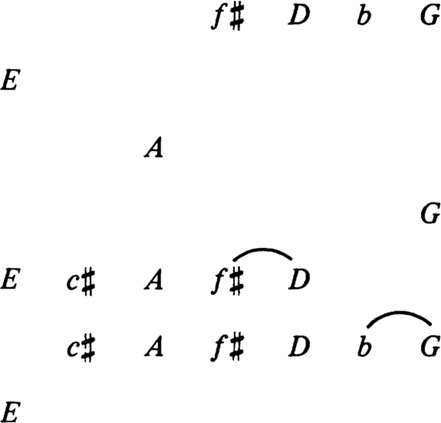
Figura 8
Análise
do trecho do Intermezzo Op. 119, no. 1, de Brahms em relação ao SR de Lá
maior dual.
O E é, portanto, exclusivamente
liberado da tensão maiúsculas/minúsculas, e, de fato, o encontraremos usado
para iniciar material cadencial seguindo
imediatamente a passagem em questão, agora que as listas canônicas completas de
ambos Fá# menor dual e Lá maior dual foram expostos. O
leitor que consultar a partitura verá o singular caráter de pivô do ., confirmado pelas semicadências
elididas, em Fá# menor dual no compasso 4 e em Lá maior dual no compasso 6:
ambas as cadências começam do E crucial com música similar.
A relação nesta peça entre as listas canônicas de Fá# menor dual
e Lá maior dual exemplifica uma transformação que chamaremos mais tarde de
“deslocamento”. Cada lista pode ser deslocada para a outra, movendo-a, por
assim dizer, um estágio adiante para sua esquerda ou direita, letras maiúsculas
e minúsculas sendo ajustadas de acordo. Vide a Fig. 9.
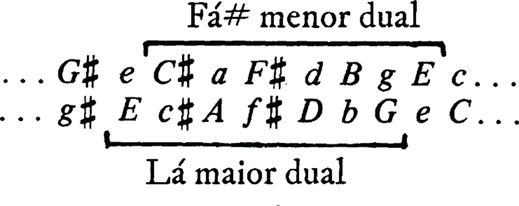
Figura
9
Relação
de deslocamento entre Fá# menor dual e Lá maior dual
O Ex. 4 mostra o sujeito da Fuga em Dó# maior do Livro II do Cravo
Bem-temperado de Bach, junto com uma versão desse sujeito transformada
por “inversão tonal na quinta.” Em nossa terminologia, a relação é, ao invés
disso, de retrogradação, obtida entre as estrutura
das tríades de Dó# maior e Sol# maior dual. Vide a Fig. 5. A situação é
claramente típica: “inversão tonal na quinta” vai retrogradar estruturas
maiores ou menores em estruturas maiores duais ou menores duais, e vice-versa.

Exemplo
4
Sujeito
da Fuga em Dó# maior do Livro II do Cravo Bem-temperado de Bach.
O Ex. 5 é interessante, neste contexto,
porque ele apresenta tal relação (envolvendo um motivo semelhante,
curiosamente) entre duas obras diferentes, mas relacionadas, do mesmo
compositor. O Ex. 5 mostra aspectos dos temas dos dois movimentos de Danças Germânicas de Beethoven. O primeiro, em Sol maior,
é da Sonata para Piano op. 79. A segunda em “Ré
maior dual”, é do Quarteto de Cordas op. 130.’[15] O primeiro segmento termina com uma appoggiatura para a harmonia subdominante de Sol maior. O segundo
segmento da mesma forma (ou “duplamente”) termina com uma appoggiatura para
harmonia “subdominante” de Ré maior dual. O leitor, se confuso com a última
frase, pode rever a Definição 2 e aquelas que a seguem para verificar que Af#D é
de fato a “tríade subdominante” do Sistema Riemann cuja lista canônica é Af#DbGeC, ou seja, de Ré maior
dual.

Exemplo 5
Comparação
entre trecho da Sonata para Piano op. 79 e do Quarteto de Cordas op. 130, ambos
de Beethoven.
O Ex. 6 mostra o tema da Rapsódia sobre um Tema de Paganini op.
43, de Rachmaninoff, junto com alguns aspectos
da Variação XVIII. A situação é complicada aqui pela relação tonal remota e
também pelo uso de f# e g# no tema original. Mesmo
assim, a técnica melódica claramente exemplifica a noção de que inverter um
sistema menor produz um sistema dual maior, assim como inverter um sistema
maior produz um sistema dual menor. A ideia de Lá♭ maior dual para a variação
é suportada harmonicamente: justamente no ponto onde o tema se move harmonicamente
de dominante para tônica (veja o Ex. 6), a variação também se move da harmonia
“dominante” para tônica (veja o Ex. 6). Deve-se, claro, lembrar que .♭.♭.♭
é a harmonia “dominante” do Sistema Riemann cuja lista canônica é .♭cA.fD♭.♭.♭,
isto é, o de Lá♭ maior dual.

Exemplo
6
Tema
e da Rapsódia sobre um Tema de Paganini op. 43, de Rachmaninoff e alguns aspectos de sua Variação XVIII.
O grupo deslocamento. Ligado à nossa
análise do Intermezzo de Brahms, que introduziu a
ideia de “deslocar” a lista canônica para um Sistema Riemann até a lista
canônica para outro, a Fig. 9 apresentou os sistemas de Fá#
menor dual e Lá maior dual em uma relação de deslocamento. O deslocamento,
naquele caso, foi de apenas uma posição, ao longo de uma lista estendida.
Podemos generalizar essa situação a nosso favor.
Dado um número inteiro N, positivo, zero ou negativo, vamos definir
uma operação formal de DESLOC(N), que opera em qualquer SR dado para produzir
um SR transformado cuja lista canônica é “deslocada N lugares” em relação
àquela do Sistema dado. Seja (T, d, m) um SR amostra, e escrevamos m’ ao invés
de d-m. A lista canônica para (T, d, m) abrange os
seis intervalos sucessivos m, m’, m, m’, m, m’. Vamos agora imaginar essa lista
canônica estendida indefinidamente, tanto para frente quanto para trás, de
forma a gerar uma alternância indeterminada de intervalos sucessivos m e m’. A
lista canônica para o Sistema deslocado por N é aquela série de sete notas que
aparece como um segmento da lista estendida N estágios à direita da lista
canônica original. Se N é negativo, “N estágios para a direita” será
interpretado como “-N fases para a esquerda.” Se N for ímpar, será necessário
imaginar os papéis conceituais de maiúsculas e minúsculas revertidos na
visualização da lista canônica para o sistema transformado. (Se entende que
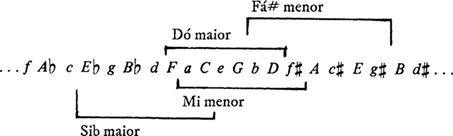
esta reversão não afeta a afinção). A Fig. 10 ilustra
essas ideias, usando o Sistema Riemann de Dó maior como ponto de referência.
Na Fig. 10, podemos ler as relações entre Si
bemol maior = DESLOC (-4)(Dó maior), Fá# menor = DESLOC(4)(Mi menor), Mi menor = DESLOC(5)(Si♭
maior), e assim por diante. Para os sistemas menores em questão, podemos
imaginar os papéis conceituais de maiúsculas e minúsculas revertidos nas listas
canônicas afetadas, tal como aparecem na Fig. 10. Em certos sistemas de afinação,
isso pode exigir mais sutilezas da notação; por exemplo; em um
afinação justa a nota escrita “.” na Fig. 10 não irá pertencer a
exatamente a mesmo classe de altura da nota escrita “.” na mesma figura. No
entanto, não iremos nos preocupar com tais problemas de notação aqui.
Figura
10
Relações
de deslocamento entre os SR’s de Dó maior Mi menor
Fá# menor e Si♭ maior
Observando a Fig. 10 e imaginando a sua estrutura generalizada
para aquela de uma lista estendida para um (T, d, m) genérico,
podemos ver como calcular o efeito de DESLOC(N) em (T, d, m). Primeiro, se . é par, vemos que o Sistema deslocado terá os mesmos
intervalos dominante e mediante do original, e a nova nota tônica será a nota
tônica antiga deslocada N lugares ao longo da lista, e, portanto, transposta
por (N/2) dominantes. Assim DESLOC(N)(T, d, m) = (T+i, d, m),
onde o intervalo de transposição é i = (N/2)d.
Observe que o intervalo de transposição depende não apenas de ., mas também do
intervalo dominante . do Sistema no qual o deslocamento está operando.
Segundo, no caso N = 1, podemos ver
que o Sistema deslocado terá o intervalo dominante d, o intervalo mediante de m’ = d-m, e a nota tônica T+m, ou seja, a nota mediante do Sistema original. Assim, DESLOC(1)(T,
d, m) = (T+m, d, d-m).
Finalmente, se N é um número ímpar qualquer, podemos escrever
DESLOC(N) = DESLOC(1)DESLOC(N-1) em termos
operacionais. Isto é, DESLOC(N)(T, d, m) =
DESLOC(1)((DESLOC(N-1)(T, d, m)). Como N-1 é par, nós vimos que DESLOC(N1(T, d, m) = (T+i, d, m),
onde i = ((N-1)/2)d. O Sistema que nós queremos é, portanto, DESLOC(1)(T+i, d, m) que, como vimos no parágrafo anterior, é (T+i+ m, d, d-m). Podemos resumir
todos os cálculos anteriores em uma definição formal.
DEFINIÇÃO 12. A
operação de “deslocar por N lugares” um sistema Riemann (T, d, m) é executado
algebricamente da seguinte forma: se N é par, DESLOC(N)(T, d, m) = (T+i, d, m), onde i = (N/2)d. Se N é ímpar, DESLOC(N)(T, d,
m) = (T+i+m, d, d-m), onde
i = ((N-1)/2)d).
Se deslocarmos por . lugares o
resultado do deslocamento de um determinado SR por .
lugares, o resultado terá de ser deslocado por um deslocamento líquido de (M+N) lugares. Isso se intui facilmente observando a Fig.
10 e a generalizando. (Deve-se lembrar que um valor negativo de
. ou . significa um deslocamento à esquerda por
(-M) ou (-N) lugares.)
A nossa intuição, isto é, argumenta pela validade da equação operacional DESLOC(M)DESLOC(N) = DESLOC(M+N). A verdade da equação
pode ser verificada formalmente usando as técnicas padrão de substituição e
álgebra em conjunto com a Definição 12. (Ao leitor é pedido, no entanto, para
que renuncie esse exercício, que envolve tomar separadamente todos os subcasos
possíveis que dependem dos M’s serem pares ou ímpares
e dos N’s serem pares ou ímpares.) DESLOC(0) é, claramente, a operação identidade IDENT em Sistemas Riemann. Segue-se que DESLOC(N)DESLOC(-N) = DESLOC(0) = IDENT;
daí, segue-se que a DESLOC(-N) é a operação inversa
de DESLOC(N). Observamos que o resultado de se
aplicar uma operação de deslocamento em seguida da outra é (operacionalmente
igual a) uma operação de deslocamento; também observamos que cada operação de
deslocamento tem uma operação inversa que é também uma operação de
deslocamento. Consequentemente, as operações de deslocamento formam um grupo
matemático.
DEFINIÇÃO 13. O
grupo que compreende todas as operações de forma DESLOC(N) será chamado de grupo deslocamento de operações sobre Sistemas Riemann;
ele será denotado por GDESLOC.
Pode haver um número finito ou infinito de formas deslocadas de
um dado Sistema Riemann, dependendo do tamanho exato de seus intervalos
dominante e mediante. A afinação é importante neste contexto. Por exemplo, é
claro que se considerarmos a Fig. 10 em afinação justa, não
haverá duplicação exata de classes de altura na lista estendida; portanto,
haverá um número infinito de Sistemas tanto maiores quanto menores entre as
formas deslocadas de Dó maior. Também haverá um número infinito (ainda maior)
de sistemas justos maiores ou menores que não são formas deslocadas de Dó maior
justo, a saber, todos os Sistemas justos maiores ou menores cuja tônica não
puder ser derivada a partir da nota C adicionando-se ou subtraindo-se quintas
justas ou terças maiores justas módulo a oitava. Embora tais Sistemas sejam, de
fato, transposições de Dó maior justo, ou de Lá maior
justo, as relações transpositivas não têm significado
funcional no contexto da Sistemática Riemann. Observe, particularmente, que o
Sistema de “Dó menor justo”, que podemos ler na Fig. 10 como Dó maior deslocado
-7 lugares, não é o Sistema conjugado de Dó maior
justo, já que o c minúsculo e o C maiúsculo na Fig. 10 diferem, em afinação
justa, por um coma sintônico.
Por outro lado, se considerarmos a Fig. 10 no temperamento igual
fica claro que existirão apenas 24 Sistemas Riemann distintos cujas listas
canônicas estarão incorporadas à lista estendida; essa lista irá repetir-se
indefinidamente, a cada 24ª entrada. Neste caso, qualquer Sistema menor
envolvido será, de fato, o conjugado do Sistema maior envolvido que tem a mesma
nota tônica, e vice-versa. No entanto, mesmo nesta pequena família de 24
Sistemas Riemann, DESLOC(-7) e CONJ operam com efeito diferente. Isto é, enquanto
Dó menor, neste contexto, é igualmente DESLOC(-7) = (Dó maior) e CONJ(Dó
maior), não é verdade que Dó maior é tanto DESLOC(-7)(Dó
menor) quanto CONJ(Dó menor). Ao invés disso, Dó
maior é DESLOC(7)(Dó menor); DESLOC(-7)(Dó
menor) não é Dó maior, mas sim Dó♭ maior = Si maior. Assim,
as operações DESLOC(-7) . CONJ não têm o mesmo efeito em todos os 24 Sistemas
Riemann em questão.
Para outro exemplo, vamos estudar o Sistema de (C, 3, 7) no
temperamento igual e inspecionar suas formas deslocadas. Vê-se que a lista
canônica AeCgE♭.♭.♭ vai se estender para a
direita da mesma forma que . . . .♭AeCgE♭. . . . A lista estendida é,
assim, uma ordenação serial do conjunto de uma escala octatônica
que se repete a cada oitava entrada ad infinitum.
Por isso, haverá apenas oito formas deslocadas de (., 3, 7). (., 3, 7) irá
reaparecer como DESLOC(8)(.,
3, 7). No entanto, seu Sistema conjugado (., 3, 8) não aparecerá entre as suas
formas deslocadas. Deslocamentos ímpares de (., 3, 7) irão, de fato, produzir
Sistemas com intervalos dominante e mediante 3 e 8, respectivamente, mas as
notas tônicas disponíveis para esses Sistemas serão apenas E, G, B♭ e .♭,
nunca .. A lista canônica estendida impõe uma certa ordenação simétrica à
escala octatônica, um recurso que pode ter
interessantes implicações analíticas e composicionais.
Voltemos para a fórmula básica DESLOC(M)DESLOC(N)
= DESLOC(M+N), e para o caso especial DESLOC(N)DESLOC(-N)
= DESLOC(0) = IDENT. Se .
e . forem ambos pares, então M+N . -N também serão pares. Podemos concluir que os
deslocamentos pares, combinando-se entre si, formam um grupo de operações. Os
matemáticos o chamariam de um “subgrupo” de GDESLOC.
DEFINIÇÃO 14. A
família de todas as operações DESLOC(N) tal que N é par será chamada de grupo deslocamento par e denotada por GDESLOCPAR.
É claro a partir da Definição 12 que as formas deslocadas por
N’s pares de um SR (T, d, m) serão precisamente
todas as transposições desse Sistema por um número qualquer de seus próprios
intervalos dominante .. Deve-se reconhecer o
importante papel GDESLOCPAR no contexto da teoria
tonal.
Entre os deslocamentos pares, DESLOC(2) e o seu inverso DESLOC(-2)
gozam de um status especial. Eles transformam um dado Sistema (T, d, m), respectivamente, em seu “Sistema dominante” (T+d, d, m) e em seu “Sistema
subdominante” (T-d, d, m).
Essas transformações interagem de um modo tão idiomático com as relações
construtivas das tríades primárias com (T, d, m) que
faz sentido dar a essas operações nomes especiais. Podemos também dar nomes
especiais para DESLOC(1) e
DESLOC(-1).
DEFINIÇÃO 15. Como
sinônimos para DESLOC(1), DESLOC(2), DESLOC(-1),
DESLOC(-2) iremos escrever MED, DOM, SUBM e SUBD respectivamente. Essas são as
operações “mediante”, “dominante”, “submediante” e
“subdominante” que transformam, respectivamente, um dado Sistema Riemann (T, d,
m) em seu “Sistema mediante” (T+m, d, d-m), seu “Sistema dominante” (T+d,
d, m) seu “Sistema submediante” (T-d+m,
d, d-m) e seu “Sistema subdominante” (T-d, d, m).
Qualquer conjunto de operações que contenha DOM deve também conter DOM DOM, DOM DOM DOM, e assim por diante; ele deve
também conter SUBD,
o inverso do DOM,
e, portanto, também SUBD SUBD, e assim por diante; portanto,
deve conter toda operação de deslocamento par. Neste sentido, podemos dizer que
DOM “gera” GDESLOCPAR. De forma análoga, MED gera GDESLOC.
Algumas outras
transformações inversivas. Enquanto MED . SUBM generalizam
formas de se relacionar os Sistemas de Dó maior e Lá menor entre si, nenhuma
dessas transformações generaliza a relação simétrica que entendemos como “tomar
a tonalidade relativa.” Isso é, Dó maior e Lá menor são “relativas” uma da
outra, mas nem MED nem SUBM expressam
adequadamente a reciprocidade desta relação. Dó maior = MED(Lá maior), mas Lá menor ≠ MED(Dó maior); Lá menor = SUBM(Dó
maior), mas Dó maior ≠ SUBM(Lá menor).
Para obter uma operação simétrica que transforma Sistemas tonais
“relativos” de forma indiferente um no outro e que seja formalmente plausível
no contexto geral do presente estudo iremos generalizar a noção da relação Parallelklang de Riemann. Em conexão com Dó maior utiliza-se Mi menor
dual, ao invés de Lá menor; invertem-se, então, as
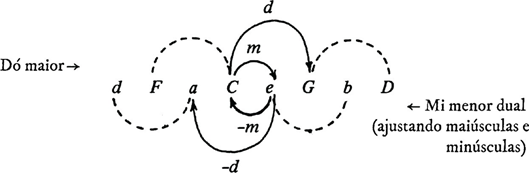
tríades, listas e Sistemas de Dó maior e Mi menor dual, uns nos outros. A Fig.
11 ilustra essa ideia.
Conforme a Fig. 11 mostra, a relação de
inversão troca as notas tônica e mediante dos Sistemas envolvidos: a nota
tônica de um torna-se a nota mediante do outro e vice-versa. Então, podemos
chamar operação generalizada de “inversão tônica-mediante” ou “inversão-TM.”
DEFINIÇÃO 16.
Inversão-TM é aquela operação INVTM que transforma um dado SR no Sistema
Riemann SRINVTM(T, d, m) = (T+m,
-d, -m).
Figura
11
Intervalos
em um exemplo de inversão tônica-mediante
A correção da definição algébrica pode ser vista observando a
Fig. 11 e generalizando a imagem. De forma semelhante, podemos definir uma
“inversão mediante-dominante.”
DEFINIÇÃO 17.
Inversão-MD é aquela operação INVMD que transforma um dado SR no Sistema
Riemann INVTM(T, d, m) = (T+d+m,
-d, -m).
A nota dominante do Sistema transformado aqui é a (T+d+m+(-d)) = T+m,
ou seja, a nota mediante do Sistema original. A nota mediante do Sistema
transformado, é (T+d+m)+(-m) = T+d, isto é, a
nota dominante do Sistema original. INVMD transforma
Dó maior dual em Si menor e Si dual menor em Dó maior. Isto é, em sistemas
maiores e menores duais ela corresponde formalmente à operação Leittonwechsel de Riemann. É claro, INVMD não
tem implicações gerais envolvendo condução de vozes, como tem a Leittonwechsel.
Já estudamos agora três operações de inversão particulares em
Sistemas Riemann, INVTD, INVTM e INVMD. Cada uma
generaliza, ao menos formalmente, uma relação apontada por Riemann como
importante ao relacionar Sistemas maiores e menores duais entre si. Para além
disso, estas três inversões em particular possuem status especial e
privilegiado na teoria generalizada. Cada uma das três mantém invariável uma
das três díades incorporadas à tríade tônica de um determinado Sistema,
transformando-a em uma díade de função equivalente na tríade tônica do Sistema
transformado. INVTD mantém invariante a díade
tônica-e-dominante, INVTM a díade
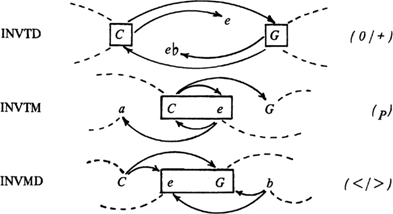
tônica-e-mediante, e INVMD a díade mediante-e-dominante. A Fig. 12 ilustra
essas propriedades, usando Dó maior e seus Sistemas transformados como
exemplos. Em cada caso, usei uma caixa para indicar a díade invariante. Os
nomes das transformações aparecem à esquerda da Fig. 12; na
direita escrevi os símbolos riemanianos convencionais
para as relações tonais envolvidas, para indicar como nossas transformações
generalizam as dele.
Figura
12
Inversões
de díades das tríades principais nas operações INVTD INVTM e INVMD e em suas
contrapartes riemanianas
Considerações variadas
adicionais. As transformações estudadas até agora se combinam entre si em
uma variedade de formas, algumas simples e outras complicadas. Por exemplo DOMINVMD(T, d, m) = DOM(T+d+m, -d, -m),
pela Definição 17; a última = (T+d+m+(-d),
-d, -m) = (T+m-d-m), que por sua vez é INVTM(T, d, m), pela Definição 16. Portanto DOM INVMD = INVTM. De forma semelhante, pode-se mostrar
que INVMD SUBD = INVTM, que INVMD
= SUBD INVTM = INVTM DOM, que INVTM INVMD = DOM,
e que INVMD INVTM = SUBD. O leitor irá lembrar-se
da importância intuitiva de tais equações operacionais. A última equação acima,
por exemplo, afirma que a inversão-MD da inversão-TM de qualquer Sistema
Riemann é o Sistema subdominante desse Sistema.
A partir das equações que acabamos de discutir, junto com o fato
de que INVTM é a sua própria inversa, segue-se que deslocamentos pares
juntamente com transformações de forma DESLOC(2N) INVTM constituem um grupo de
operações. O grupo contém INVMD, assim como INVTD, já que INVMD = DESLOC(-2) INVTM. Quando aplicado a Dó maior, os membros
deste grupo geram Sol maior, Fá maior, Ré maior, e assim por diante, como as
formas deslocadas por N pares de Dó maior, e também Mi menor dual, Si menor
dual, Lá menor dual, Fá# menor dual, e assim por diante, como as formas
deslocadas por N pares de INVTD(Dó maior). Qualquer um destes Sistemas é uma
“forma” de qualquer outro, módulo este grupo.
Outra rede de inter-relações razoavelmente simples entre as
nossas transformações surge do fato de que DOM CONJ = CONJ
DOM (a validade da equação pode ser estabelecida pelas técnicas usuais).
Segue-se que os deslocamentos pares, em conjunto com as transformações de forma
DESLOC(2N) CONJ, constituem um grupo de operações.
As formas de Dó maior, mod este grupo, são Dó maior,
Dó menor, Sol maior, Sol menor, Fá maior, Fá menor, e
assim por diante. Qualquer um destes Sistemas é uma forma de qualquer outro,
módulo o grupo.
Outro grupo interessante compreende todos os deslocamentos
juntamente com todas as transformações de forma DESLOC(N) RET. Pode-se provar
que o DESLOC(N) RET = RET DESLOC(-N). As listas canônicas para as várias formas
de um determinado Sistema, mod deste grupo, são os
vários segmentos de sete notas da lista canônica estendida, lidos de frente
para trás, ou vice-versa. Portanto, as formas de Dó maior, por exemplo, são Dó
maior, Sol maior dual, Mi menor, Si menor dual, Lá menor, Mi menor dual, Sol
maior, Ré maior dual , Fá maior, Dó maior dual, etc.
As transformações INVTM e INVMD são membros deste grupo, uma vez que INVTM = DESLOC(1) RET e INVMD = DESLOC(-1) RET. (As equações podem
ser provadas da forma habitual. O formato visual da Fig. 11, quando
generalizado, torna a validade da equação acima intuitivamente evidente.)
Outras formas de combinar as transformações em questão levam a
transformações mais remotas e a grupos de operações maiores e mais complexos.
Por exemplo, vamos temporariamente definir uma operação X: transpor um
determinado Sistema Riemann por seu intervalo mediante. Assim, X(Dó maior) = Mi maior, X(Dó menor) = Mi♭
menor, e assim por diante. Em geral, (T, d, m) = (T+m,
d, m). Vamos também definir Y: transpor um determinado Sistema Riemann pelo seu
intervalo dominante-menos-mediante. Assim, Y(Dó maior)
= Mi♭ maior, Y(Dó menor) = Mi menor, etc. Em geral, (T, d, m) = (T+d-m, d, m). Pode-se provar que as equações a seguir são
verdadeiras. CONJ MED = X, MED CONJ = Y, INVTM INVTD = Y, INVMD INVTD = o
inverso de X, e assim por diante. Disso segue: qualquer grupo que contenha CONJ
e MED deve conter ambos X e Y; da mesma forma, qualquer grupo que contenha INVTM,
INVMD e INVTD deve conter ambos X e Y, e assim por diante. Qualquer grupo que
contenha X e Y deve conter a operação Z = Y-inversa X. Já que X transpõe o
Sistema (T, d, m) por m e Y-inversa transpõe o Sistema resultante pelo
complemento de m’, que é m-d, Z transpõe o dado Sistema por m-m’,
ou seja, por m-(d-m) ou 2m-d. Z, por exemplo, leva Dó
maior a Dó# maior e Dó menor a Dó♭ menor. Deixando uma
exploração mais aprofundada de tais transformações “pós-Wagnerianas”
generalizadas para aqueles que possam estar interessados, passemos agora a
outro tópico.
DEFINIÇÃO 18. O tipo do Sistema Riemann (T, d, m) é o par ordenado de
intervalo (d, m). Dois Sistemas Riemann “têm o mesmo tipo” ou “são do mesmo
tipo” se eles tiverem o mesmo intervalo dominante e o mesmo intervalo mediante.
Assim, Dó maior e Fá# maior são do mesmo tipo, supondo a mesma
afinação. No temperamento igual de doze alturas, (., 2, 5) e (.♭,
2, 5) são do mesmo tipo, a saber, o tipo (2, 5). Também do tipo (2, 5) é (C+j, 2, 5), onde j representa
uma quinta justa. O conceito de tipo nos permite relacionar a estrutura
intervalar de (C+j, 2, 5)
com a estrutura intervalar de (., 2, 5), sem ter que atribuir qualquer
significado funcional para a relação transpositiva
entre eles.
O conceito de tipo é também útil para fazer generalizações sobre
as estruturas intervalares de Sistemas que são funcionalmente relacionados, sem
ter de se preocupar com suas notas tônicas. Por exemplo, dado qualquer SR (T,
d, m), o seu Sistema conjugado será de tipo (d, d-m),
assim como seus sistemas deslocados por N ímpares. Nesse sentido, podemos dizer
que os Sistemas deslocados por N ímpares são todos de “tipo conjugado” mesmo
que o Sistema conjugado em si não apareça como um Sistema deslocado.
Em sentido semelhante, podemos dizer que as formas
TD-invertidas, as TM-invertidas e MD-invertidas de (T, d, m) são todas de um
mesmo tipo, ou seja, (-d, -m), o “tipo invertido” de (d, m). E podemos dizer
que qualquer Sistema menor é “de tipo retrógrado” em relação a qualquer Sistema
menor dual, de maneira similar. Para fazer tal discurso formalmente preciso,
precisamos apenas definir as operações de conjugação, inversão e retrogradação em tipos.
DEFINIÇÃO 19. Dado
um tipo (d, m), o tipo conjugado é conj(d,
m) = (d, d-m). O tipo invertido
é inv(d,
m) = (-d, -m). O tipo retrógrado é ret(d, m)
= (-d, m-d). O grupo que compreende as três operações conj,
inv e ret, junto com a
operação identidade ident, será chamado de “grupo
serial de operações-de-tipo” em tipos de Sistemas.
É fácil verificar que as operações definidas formam um grupo. Se
verifica que as equações entre elas são análogas àquelas que foram agrupadas na
Tab. 3 para as operações-de-Sistema análogas; o análogo da
Tab. 3 é válido para estas operações-de-tipo.
O grupo serial de operações em tipos é de fundamental
importância. Vê-se que todas as operações que examinamos até agora, até mesmo
as nossas exóticas operações “pós-Wagnerianas”, levam Sistemas Riemann a
Sistemas Riemann de tipo idêntico, conjugado, invertido ou retrógrado.
Passemos novamente para outro tópico. É interessante notar que
as categorias riemannianas de Uberklang
e Unterklang podem ser generalizadas em nossa
terminologia presente, pelo menos formalmente.
DEFINIÇÃO 20. O SR
(T, d, m) será chamado de “direcionado para cima” quando, dado uma altura
representando a classe de altura T, a próxima altura acima representando T+m acima é mais grave que a próxima altura acima
representando T+d. O SR (T, d, m) será chamado de
“direcionado para baixo” quando, dado uma altura representando a classe de
altura T, a próxima altura abaixo representado T+m é
mais alta que a próxima altura abaixo representando T+d.
O tipo (d, m) será chamado de “direcionado para cima/para baixo” se todos os
Sistemas Riemann daquele tipo forem direcionados para cima/para baixo.
Pode-se verificar que todo SR é direcionado para cima ou
direcionado para baixo, mas não ambos. O mesmo é verdade para todos os tipos. O
conjugado de qualquer Sistema ou tipo é direcionado no mesmo sentido que aquele
Sistema ou tipo; Sistemas invertidos ou retrógrados são direcionados no sentido
contrário.
É quase desnecessário ressaltar que há importantes tradições na
teoria tonal que o trabalho deste artigo não generaliza. A mais significativa
destas tradições envolve o estudo de condução de vozes e do contraponto em
relação à funcionalidade tonal; nossa teoria, com suas listas canônicas, deve
forçosamente permanecer calada em relação a tais questões em geral, apesar de
se poder, é claro, desenvolver protocolos para a condução de vozes e o
contraponto ligados a Sistemas Riemann específicos que não os tonais.
A literatura de outra importante tradição expõe certos sistemas
em que se mede vários intervalos harmônicos de interesse (oitavas, dominantes,
mediantes) não como vindos de um gerador, mas indo a um gerado comum. Para ver
a distinção, note que nosso formalismo nos permitiu analisar a tríade menor
como compreendendo uma quinta “acima” e uma terça menor “acima” a partir de um
gerador comum (por exemplo, de C para G e de C para e♭).
Nosso formalismo também nos permitiu analisar a tríade menor como uma estrutura
“dual”, constituída por uma quinta “abaixo” e uma terça maior “abaixo” a partir
de um gerador comum (por exemplo, de G para C e de G para e♭ ). Mas o nosso formalismo não nos habilitou e não pode nos
habilitar a analisar a tríade menor como constituída de uma quinta “para cima”
e uma terça maior “para cima” em direção a um gerado comum (por exemplo, de C
para G e de e♭ para G).
Sistemas envolvendo relações gerados-comuns, sejam ligados a
tríades menores ou em outros contextos, podem ser chamados de “fônicos”, em
oposição a “sônicos.”[16] Um formalismo mais
geral ainda que o do presente artigo talvez pudesse ser desenvolvido para
generalizar sistemas intervalares fônicos e sônicos e interrelacionar
todos os sistemas, tanto fônicos quanto sônicos, entre si e uns com os outros.
No entanto, as formalidades do presente artigo são, imagino, amplamente gerais
para satisfazer a maioria dos leitores por enquanto.
REFERÊNCIAS
BORETZ, Benjamin. “Musical Syntax
(II)”. Perspectives of New Music,
v.10, n.1, 1971.
COHN, R. Lewin, David. Grove Music Online,
20 jan. 2001 (atualização em 27 ago. 2003). Disponível em: https://doi.org/10.1093/gmo/9781561592630.article.47754.
Acesso em: 13 abr. 2022.
FORTE, Allen. The Structure
of Atonal Music. New Haven e Londres: Yale University Press, 1973.
HAUPTMANN, Moritz. Die Natur
der Harmonik und der Metrik. Leipzig: Breitkopf
und Haertel, 1853.
LEWIN, D. Behind the Beyond:
A Response to Edward T. Cone. Perspectives of New Music, Vol. 7, nº 2, p. 59-65. Seattle: Perspectives
of New Music, 1969.
LEWIN, D. Music Theory,
Phenomenology, and Modes of Perception.
Music Perception: An Interdisciplinary Hournal Vol. 3,
nº 4, p. 327-392. Oakland: University of California Press, 1986.
LEWIN, D. Musical Form
and Transformation:
Four Analytic Essays. New
York: Oxford University Press, 1993.
LEWIN, D. Generalized Musical Intervals and
Transformations, 2ª ed. New York: Oxford University Press, 2007. 288 p.
MICKELSEN, William C. Hugo Riemann’s Theory of Harmony. Lincoln and
London: University of
Nebraska Press, 1977.
MISCH, Ludwig. Alla danza tedesca. Beethoven Studies,
trans. G. I. C. DeCourcy. Norman: University
of Oklahoma Press, 1953.
OETTINGEN, Artur von. Harmoniesystem in dualer Entwicklung
Leipzig: W. Glaser, 1866.
HINDEMITH, Paul. The Craft
of Musical Composition,
trad. Arthur Mendel. London: Associated Music Publishers,
1942.
RAMEAU, Jean-Phillipe. Traité de l’harmonie réduite
à ses príncipes naturels.
Paris: Ballard, 1722.
RAMEAU, Jean-Phillipe. Nouveu système de musique théorique et pratique. Paris: Ballard,
1726.
RAMEAU, Jean-Phillipe. Generátion harmonique. Paris: Prault, 1737.
RAMEAU, Jean-Phillipe. Démonstration du principe
de l’harmonie. Paris: Durand,
1750.
WESTERGAARD, Peter. An Introduction to
Tonal Theory. Nova Iorque: W. W. Norton & Company, Inc., 1975.
ZARLINO, Gioseffo. Le Institutioni Harmoniche.
3. ed. Veneza: Senese, 1573.
Notas
2 N.T. Dominant interval, no original.
Tanto “intervalo dominante” quanto “intervalo de dominante” são traduções
possíveis, sendo que a segunda parece ser a forma mais comum na qual o termo
aparece em português. Dado que, neste artigo, um conceito de dominante externo
à sistemática elaborada não é relevante para a construção das tríades do
sistema, não vejo justificativa para o uso da preposição, já que esse indicaria
a relevância tal conceito. Em outras palavras, neste contexto, os intervalos
não são de uma função (pré-existente), ao invés disso, eles determinam o que é
aquela função. Considerações análogas valem para a traduções que envolvem as
demais funções (mediante, subdominante, etc) e que
utilizam “tríade” no lugar de “intervalo”.
3 N.T. Lewin utiliza,
neste artigo, sempre a notação germânica para se referir às classes de altura.
As “notas de solfejo” (Dó, Ré, Mi, etc.) serão utilizadas doravante quando
associadas aos adjetivos “maior” e “menor”, enquanto a notação germânica será
mantida para os demais casos, em especial para a aritmética dos Sistemas
Riemann.
4 Uma bibliografia e
crítica de escritos de e pertinentes a Riemann, conveniente para leitores
americanos, pode ser encontrada em Mickelsen (1977). Entre a variedade de obras fornecendo
fundação para a abordagem escolhida por Riemann e continuada nas formalidades
deste artigo, deve-se chamar particular atenção para o trabalho de
Jean-Phillipe Rameau
(1726) em seu Nouveau système de musique théorique et pratique. Aqui Rameau
cunha a palavra “subdominante”. Ele analisa a importância da relação
proporcional: a fundamental da subdominante está para a fundamental da tônica
assim como a fundamental da tônica para a fundamental da dominante. Essa
relação pode ser vista como subjacente ao aspecto triádico
do método construtivo retratado na Figura 1; ele será mais tarde generalizado
pela Figura 2. No Nouveau système, Rameau analisa a escala (melhor, nosso “conjunto
diatônico”) como surgindo da conjunção de três tríades primárias, uma
características também manifesta na Figura 1 e a ser generalizada na Figura 2.
Antes dessa obra, a afirmação de Rameau de que a
melodia era subordinada teoricamente à harmonia coexistiu de uma forma bem
desconfortável com a sua adoção da escala maior Ptolemaica,
ao invés da justa. Ver Rameau (1726, livro 1, capítulo
5). Outro trabalho importante que requer citação aqui é o de Moritz Hauptmann (1853),
Die Natur der Harmonik und der Metrik. Ao adotar uma
abordagem filosófica, ao invés de numérica e acústica, para construções como a
da Figura 1, Hauptmann dá um passo considerável em
direção ao formalismo, evitando, aliás, alguns problemas metodológicos que
atormentam Rameau. Em particular, sua concepção da
tríade menor como uma “unidade negativa” filosófica ao invés de uma estrutura
acústica de “harmônicos inferiores” se mostra vantajosa em relação à concepção
de Riemann sobre a tríade, concepções que, no fim, levam para a mesma análise
formal. O formato da lista canônica na Figura 1 é tomado diretamente de Hauptmann, junto com a notação de maiúsculas e minúsculas.
Como veremos, essa notação é conveniente e sugestiva em muitos contextos. A
ideia de usar a lista canônica, ao invés da ordem escalar, como a ordenação
fundamental para o conjunto diatônico tem muitas e importantes implicações
formais, como também veremos.
5 N.T. Apesar das
restrições, o uso do termo ainda causa estranheza, já que o termo “tríade”, no
mínimo atualmente, é normalmente associado exclusivamente aos membros das
classes de conjunto de número Forte 3–10, 3–11 e 3–12. “Tricorde” é o termo
mais usual a ser empregado aqui. Lewin talvez estivesse ciente dessa
alternativa e tenha escolhido, mesmo assim, “tríade” devido às conotações do
termo enquanto uma entidade harmônica que é fundamental para um sistema tonal.
Devido a essa possiblidade, mantive o termo original. É importante notar que a
escolha do termo, no entanto, não tem impacto na formalização elaborada durante
o artigo, ainda que possa ter para a interpretação da significância dessa
formalização para a teoria musical em geral.
6 Na verdade, se
restringirmos nossa atenção ao temperamento igual de doze alturas e
questionarmos quais Sistemas Riemann têm a propriedade em discussão e também
sete notas distintas em seus conjuntos diatônicos, encontraremos essencialmente
apenas quatro desses sistemas. Um é o sistema maior tonal, por exemplo (C, 7,
4) com a lista canônica FaCeG♭D. (As notas da tríade
em questão estão em itálico). Outro é o sistema tonal “dual menor”, o qual
estudaremos mais a frente, por exemplo (G, 5, 8) com lista canônica D♭bGe♭Ca♭F.
Os outros dois sistemas são as transformações pelo círculo das quintas (ou pela
“multiplicação) dos dois acima, por exemplo (C, 1, 4) e (C#, 11, 8) com as
listas Be♭CeC#fD e D♭bC#aCa♭B.
7 N.T. Aqui e em
algumas outras passagens deste artigo Lewin utiliza “nota” no lugar de
“altura”, apesar dos termos não serem, em geral, sinônimos. Feita essa
ressalva, não indicarei as demais ocorrências dessa substituição.
8 N.T. Lewin,
curiosamente, escolhe o termo “Forte label”,
traduzido por “rótulo Forte”, ao invés do, atualmente padrão, “Forte number” (número Forte) ou ainda do menos comum “Forte name” (nome Forte). A nota de rodapé abaixo deixa claro que
o termo de refere, de fato, ao construto familiar à
teoria pós-tonal.
9 Pelo “rótulo Forte”
correspondendo a um conjunto de classes de altura, eu me refiro ao rótulo
numérico atribuído a esse conjunto no trabalho de Allen Forte (1973).
10 No que concerne a sombra histórica da Figura 3, pode-se mencionar em
particular a discussão da divisão harmônica e aritmética da quinta em conexão
com a estrutura triádica maior e menor dada por Gioseffo Zarlino (1573, livro 3, capítulo 31). A relação de
tríades paralelas maiores e menores à maneira da Figura 3 é discutida por Rameau no livro 1, capítulo 3, artigo 5 do Traité. Rameau chama a troca de m
e m’ uma “nova espécie de renversement,” significando
uma redisposição dos intervalos no registro supostamente
análogo à redisposição de alturas no registro que
produz a inversão de acordes. Essa atitude em relação ao menor seria, no
entanto, superada nos trabalhos posteriores de Rameau
por uma grande variedade de outras ideias.
11 N.T. Circle-of-fifths transforms, no
original. Obter um circle-of-fifths transform de um determinado conjunto equivale,
algebricamente, a se multiplicar (módulo 12) cada uma de suas classes de altura
por 7 (o inteiro correspondente à classe de altura da quinta justa), as levando
para a sua “posição” no círculo das quintas.
12 O temperamento igual
é apenas uma convenção notacional aqui. O trabalho que segue poderia ser
conduzido usando quaisquer outros tamanhos razoáveis de “quintas” e “terças
maiores” como intervalos de dominantes e mediantes para o Sistema maior. Seria
uma tarefa quase interminável catalogar todas as razões levantadas na história
da teoria tonal para atribuir prioridade especial a esses intervalos. Novas
razões ainda estão sendo levantadas ativamente na literatura. Peter Westergaard (1975,
p. 411-427), por exemplo, segue a grande tradição de construir a tonalidade ex nihilo em An
Introduction to Tonal Theory. Sua discussão da quinta (justa) é uma sensível e
atrativa amálgama de muitas atitudes históricas, numéricas, filosóficas e psico-acústicas. Sua discussão da terça maior, junto com o
coma sintônico e a necessidade de temperamento,
também invoca algumas ideias tradicionais. É, no entanto, único, para o meu
conhecimento, o mordaz argumento adicional que, se nós não tivéssemos um
intervalo consonante com aproximadamente esse tamanho, não conseguiríamos fazer
análises schenkerianas para os backgrounds de peças
tonais. Uma teoria recente de Benjamin Boretz (1971, p.232-270) fornece um argumento
interessante, rigorosamente anti-historicista e anti-acústico, para atribuir prioridade especial para a
quinta como o intervalo dominante na música tonal . Começando (!) com o
temperamento igual de doze alturas e certos requisitos formais para um certo
tipo de sistema musical, Boretz mostra que o
intervalo 7 é a única escolha disponível para dividir a oitava e ser ele mesmo
dividido de uma forma a satisfazer esses requisitos.
13 O leitor encontrará
uma exposição ampla dessas ideias em Mickelsen (1977). Como indicado na Nota 1, Hauptmann havia anteriormente favorecido essa análise
formal da tríade menor. O próprio Rameau (1737) havia flertado com ela temporariamente.
14 N.T. Foi mantida
nesta tradução a numeração de oitavas do original, onde C4 (e não C3) se refere
ao dó central.
15 A curiosa relação
entre os temas foi apontada por Ludwig Misch em seu
artigo “Alla danza tedesca,”
(MISCH, 1953, p. 14-18.)
16 A nomenclatura
generaliza a terminologia de Artur von Oettingen (1866). O próprio Rameau (1750)
apresentou uma teoria fônica da tonalidade menor entre as suas muitas
tentativas de reconciliar a tonalidade maior com a menor. Em tempos mais
recentes, explicações fônicas para vários fenômenos tonais foram levantadas por
Paul Hindemith (1942)
em The Craft of Musical Composition.
Autor notes
1 Felipe Defensor
Martins é Técnico em Piano Popular pelo Conservatório Musical Souza Lima e
Mestre em Teoria e Análise Musical pela Escola de Comunicação e Artes da
Universidade de São Paulo (ECA-USP). Tem como tópicos de interesse matemática
aplicada à música, filosofia da música e forma musical. Participa de um grupo
de leitura do Generalized Musical Intervals
and Transformations
composto por pesquisadores e alunos da do Programa de Pós Gradução
em Música da UFRJ e do Conservatório Musical Souza Lima.